Post

[논문] Reconstructing growth and dynamic trajectories from single-cell transcriptomics data

Reconstructing growth and dynamic trajectories from single-cell transcriptomics data

Posted Updated
By Cheong seolmo
37 min read
[논문] Reconstructing growth and dynamic trajectories from single-cell transcriptomics data

Reconstructing growth and dynamic trajectories from single-cell transcriptomics data

Abstract

  • TIGON: 동적이고 불균형한 최적 수송(optimal transport) 알고리즘. 시계열 scRNA-seq 데이터를 이용해 세포의 동적 궤적, 세포 집단 성장, GRN을 동시에 재구성하는 알고리즘
    • 서로 다른 시점의 scRNA-seq 데이터(세포를 파괴하는 방식으로 진행되는)를 Optimal Transport 이론으로 연결
      • Optimal Transport(OT): 두 시점의 세포 분포를 보고 세포들이 시간에 따라 어떻게 이동했는지 가장 효율적으로 매칭
  • 고차원 최적 수송 문제를 해결하기 위해, Wasserstein-Fisher-Rao(WFR) 거리를 기반으로 한 dimensionless formulation 사용하여 딥러닝 방식 적용
    • Wasserstein–Fisher–Rao 거리: 두 개의 확률 분포 또는 밀도 함수 사이의 차이를 측정하는 수학적 거리. Wasserstein 거리는 질량의 재배치(이동)를 고려, Fisher-Rao 거리는 질량의 증감(성장/감소)을 고려. 최적 수송 문제(Wasserstein)와 질량 변화 모델(Fisher-Rao)을 PDE 형태로 통합한 것. 이를 최소화하면 가장 경제적으로 상태 A에서 상태 B로 바뀌는 경로
      • \[\text{WFR}^2(\rho_0, \rho_1) = \inf_{\rho, \mathbf{v}, g} \int_0^1 \int_{\Omega} \left( \|\mathbf{v}(x,t)\|^2 + g(x,t)^2 \right) \rho(x,t) \, dx \, dt\]
      • 제약 조건: \(\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = \rho g\)
        • 질량 보존 법칙(이동만 존재, 질량은 보존)을 질량 생성/소멸이 있는 상황에 맞게 일반화.
  • 시뮬레이션 데이터에서 평가되고, 기존 방법보다 더 정확하고 강건하게 세포 상태 전이 및 성장 예측 가능
  • 세 개의 실제 scRNA-seq 데이터셋 활용, 시간 흐름 추론에서의 세포 성장의 중요성, 측정되지 않은 시점의 유전자 발현 재구성 능력, 시간 기반 GRN 및 세포 간 상호작용 추론에 활용 가능

similar content being viewed by others

MAIN

  • scRNA-seq 기술은 서로 다른 시점에서 세포를 샘플링하기에 세포의 동적 변화를 관찰할 수 있지만, 시퀀싱 과정에서 세포가 파괴되기 때문에 세포 간의 계통 관계나 세포의 궤적을 파악할 수 없고 개별 세포 수준에서 유전자 발현의 시간적 변화를 추적하는 것도 불가능
    • scRNA-seq와 lineage tracing(계보 추적)의 결합: 클론(유래가 같은 세포들) 간의 관계는 알아낼 수 있지만, 정밀도는 부족하고 실험실 조건(in vitro)에만 적용 가능
    • Pseudotime 분석: 발달적으로 유사한 세포들은 유전자 발현 프로파일이 비슷할 것이라는 가정을 바탕으로 세포들을 분화 궤적 상의 순서로 배열
    • RNA-velocity: spliced mRNA(스플라이싱되어 intron이 제거되고 exon만 남은 mRNA)와 unspliced mRNA의 비율을 이용하여 세포가 어떤 방향으로 상태 전이를 하고 있는지 추정
    • Cospar: 추가적인 실험적 클론 정보(시간 정보 포함)를 이용해 세포 전이 맵(transition map)을 추론
    • Dynamo: 시간 기반 대사 라벨링 데이터를 활용해 unspliced 및 spliced mRNA의 수치를 모델링해 세포 전이의 연속적인 속도장(velocity field) 재구성
    • PRESCIENT: 세포 분화를 확산(diffusion) 과정으로 모델링하여, 분화 지형(differentiation landscpae)을 학습
    • MuTrans: 다중 스케일 축소 기법(multiscale reduction)을 통해 스냅샷 데이터에서 세포들이 수렴하는 지점(attractors)과 그 사이의 전이 확률 정령화, 저차원의 동적 다양체(dynamical manifold)를 구축
      • manifold: 국소적으로 평면처럼 보이는 공간으로, 고차원 데이터를 저차원 manifold 위에 있다고 가정
    • ⟹ 대부분 정상 상태(stationarity)나 평형 상태(equilibrium)를 가정하기 때문에, 발달처럼 시간에 따라 변화하는 동적 과정 포착하지 못함
  • Fokker-Planck 방정식: 세포 집단의 동역학을 모델링하는 데 사용될 수 있지만, 파라미터 추정 및 수치 해석이 어렵고 계산 비용이 큼
  • Optimal transport(OT, 최적 수송): 두 분포 사이의 질량을 이동시키는 고전적인 수학 이론으로 최근 scRNA-seq 데이터 분석에도 활용
    • Waddington-OT: 유전자 발현 공간에서 세포들이 확률 분포에 따라 샘플링된다고 가정, 두 연속된 시간 지점 간의 세포 이동 경로(transport plan)를 OT로 추론
    • Dynamic OT: 시간 개념을 추가하여 유체역학과 연결되는 해석을 가능하게 하며, 이는 볼록 최적화 문제(convex optimization)로 귀결됨
      • Convex Optimization: 문제의 형태가 볼록한 최적화 문제. 어떤 함수를 최소화하거나 최대화하려 할 때, 함수와 조건들이 좋은 성질(볼록성)을 가지고 있으면 해를 안정적으로 구할 수 있음. 지역 최적값=전역 최적값.
    • TrajectoryNet: dynamic OT와 continous normalizing flows을 결합하여 세포 동역학의 연속적인 경로 추론
    • MIOFlow: geodesic autoencoder와 multiscale manifold distance를 사용하여, 데이터 다양체 상에서 OT 흐름을 구현함으로써 스냅샷 데이터의 확률적 동역학 학습
  • velocity: 이와 같은 모델에서는 개별 세포의 유전자 발현이 시간에 따라 순간적으로 어떻게 변하는지 설명하기 위해 velocity 개념 도입
  • 성장 항(growth term): 세포 분열과 세포 사멸 등으로 인해 전체 세포 수(population)가 시간이 지나며 변할 수 있기에 변화를 반영할 수 있는 성장 항을 모델에 포함
    • Waddington-OT와 PRESCIENT는 성장 지표 유전자(growth hallmark genes)의 발현 수준을 이용해 세포의 성장을 간접적으로 추정
    • 연구 결과로 KEGG, GO 등 서로 다른 생물학적 데이터베이스는 서로 다른 유전자 리스트를 제공하기에, 추정된 성장 결과는 데이터베이스 선택에 따라 크게 달라질 수 있음
    • TrajectoryNet은 연속적인 OT 모델 환경에서 growth/death를 별개의 이산적이고 정적(static)이며 불균형(unbalanced)한 OT 모델로 통합한 최초의 방법
  • 개별 세포 수준의 유전자 발현 속도와 전체 세포 집단의 성장을 동시에 통합할 수 있는 모델과 계산 도구는 아직 부족한 실정

1

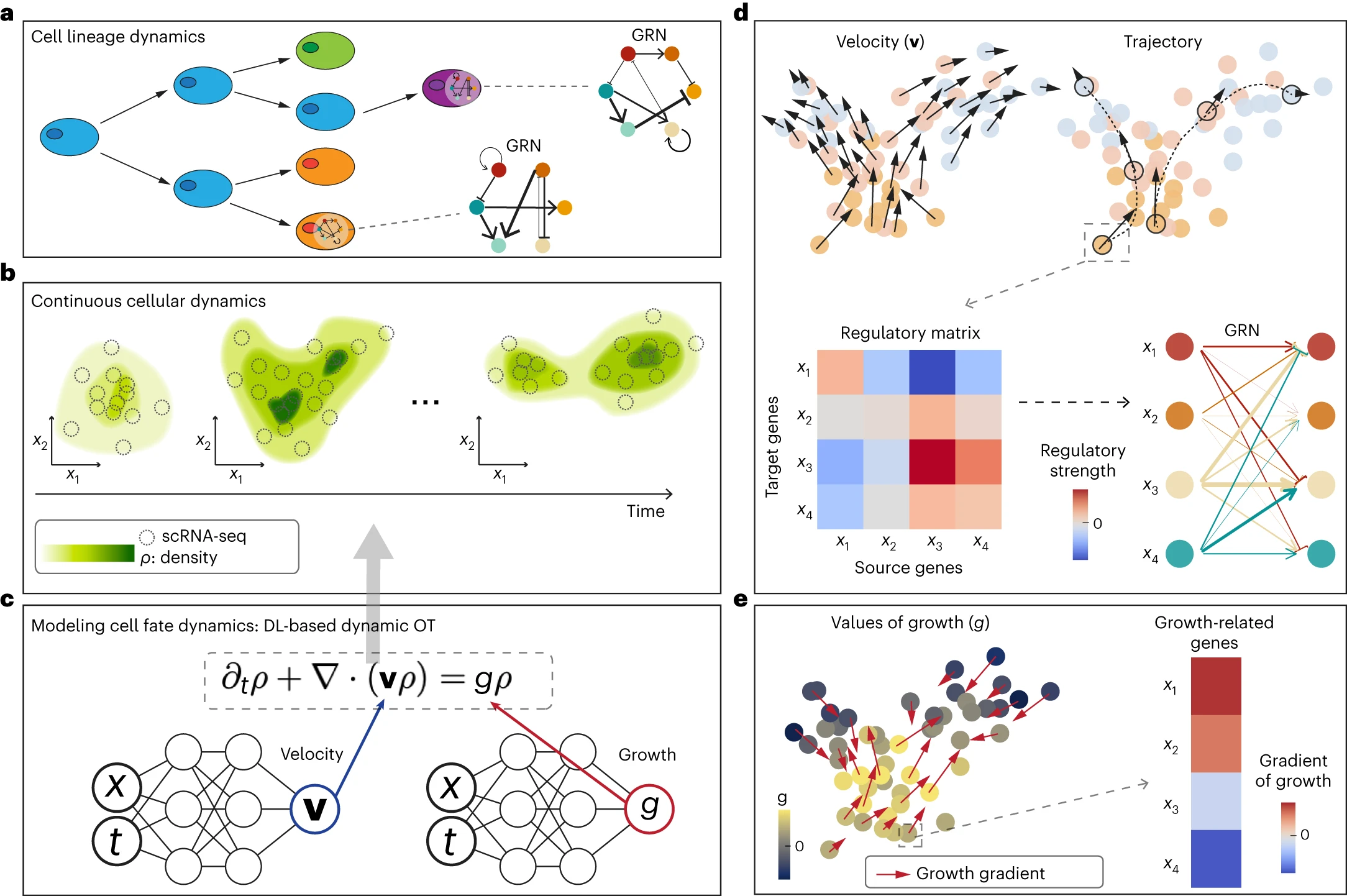
  • Fig. 1: Illustrative diagram of TIGON

    • (a): 세포 성장, 상태 전이, GRN이 포함된 세포 계통 역학 설명
    • (b): 연속적인 세포 역학
      • 세포 상태의 연속적인 변화를 시간에 따라 정의된 밀도 함수 \(ρ(x,t)\)로 설명. scRNA-seq 데이터를 입력으로 하여, 특정 시간 지점에서의 세포 상태 밀도 \(ρ\)를 추정
    • (c): 딥러닝 기반의 동역학 모델
      • 속도 \(v\)와 성장률 \(g\)가 포함된 PDE에 의해 밀도 함수 \(ρ\)결정
      • \(v\)와 \(g\)는 각각 신경망으로 모델링 되며, 딥러닝을 통해 학습
    • (d): TIGON의 출력 결과 및 후속 분석
      • 좌측 상단: 세포 속도 벡터 시각화
      • 우측 상단: 각 세포의 추적된 궤적
      • 좌측 하단: 선택된 세포 혹은 세포 유형에 대한 유전자 조절 행렬
      • 우측 하단: GRN. 화살표의 굵기는 조절 강도
    • (e): TIGON의 출력 결과 및 후속 분석
      • 좌측: 성장률 \(g\)의 추정값을 색상으로 표현한 시각화.
      • 우측: \(g\)의 그래디언트는 각 유전자가 성장 변화에 얼마나 기여하는지 나타냄. 성장 관련 유전자는 그래디언트 값이 큰 유전자들 위주로 선별
  • TIGON: 짝지어지지 않은 시계열 단일세포 전사체 데이터를 연결함으로써 세포 속도, 성장, 세포 역학을 추론하는 모델
    1. 동적 불균형 OT 모델: 개별 세포와 전체 세포 집단의 유전자 발현 속도를 동시에 포착
    2. mesh-free, dimensionless formulation: WFR 거리를 기반으로, Neural ODEs을 통해 쉽게 계산 가능
    3. 시간적, 인과적 유전자 조절 네트워크 및 성장 관련 유전자의 추론 가능
  • 시뮬레이션된 유전자 조절 모델을 통해 TIGON이 세포 속도와 성장을 하나의 통합된 프레임워크에서 효과적으로 모델링할 수 있음을 보였으며, 기존의 균형잡힌 동적 OT 모델과 비교 분석
  • 세 가지 시계열 시스템에 적용
    • 분기(bifurcation)를 포함한 계통 추적(lineage tracing) 데이터셋
    • 상피-간엽 전이(EMT, Epithelial-to-Mesenchymal Transition) 데이터셋
    • 분기를 포함한 유도만능줄기세포(iPSC) 분화 데이터셋
  • ⟹ TIGON은 세포의 속도, 궤적(trajectory), 성장률을 정확히 복원해낼 뿐 아니라 시간에 따른 GRN과 cell-to-cell communication까지 추론하는 데 성공

Results

Overview of TIGON

  • 모델에서의 세포 집단: 시간에 따라 변하는 밀도 함수 \(ρ(x,t)\)
    • \(\rho (x,t)\): 시각 \(t\)에서 유전자 발현 상태 \(x\) 상의 세포 수 분포
    • \(x \in \mathbb{R}^d\) (\(x\): 유전자 발현 상태, \(\mathbb{R}^d\): d차원의 유전자 발현 공간)
  • time-series scRNA-seq data는 주어진 이산적 시간 지점에서의 밀도 함수 \(\rho_i=\rho(x, t_i), i=1, 2, ..., T\)를 생성하는 데 사용됨. Gaussian Mixture Model 기반.

  • TIGON의 딥러닝 기반 접근법은 이러한 시간 지점에서의 밀도 \(\rho_i\)를 입력으로 하여 hyperbolic partial differential equation을 이용해 시간에 따라 연속적인 밀도 함수 \(\rho(x,t)\)를 interpolation 방식으로 재구성

  • \[{\partial }_{t}\rho \left(x,t\right)+\nabla \cdot \left(\mathbf{v}\left(x,t\right)\rho \left(x,t\right)\right)=g\left(x,t\right)\rho \left(x,t\right)\]
    • convection term \(\nabla \cdot \left(\mathbf{v}\left(x,t\right)\rho \left(x,t\right)\right)\): 세포 밀도(\(\rho\))의 이동
    • velocity \(\mathbf{v}(x,t) \in \mathbb{R}^d\): 시간 \(t\)에서의 유전자 발현 상태 \(x\)에 있는 세포들의 유전자 발현의 순간적인 변화(속도)
    • growth term \(g(x, t)\): 순간적인 세포 개체수의 변화, 즉 세포 집단의 증감
    • ⟶ 속도 \(v\)와 성장률 \(g\)가 세포 밀도의 시간적 변화(동역학)를 결정
    • WFR 비용(Wasserstein-Fisher-Rao cost)를 최적화해 불균형 최적 수송(unbalanced optimal transport, OT) 방식으로 해결
  • \[W_{0,T} = T \int_0^T \int_{\mathbb{R}^d} \left( |\mathbf{v}(x,t)|^2 + \alpha |g(x,t)|^2 \right) \rho(x,t) \, \mathrm{d}x \, \mathrm{d}t\]
    • An Interpolating Distance between Optimal Transport and Fisher-Rao: WFR 거리를 통해 유체 시스템에서 2차 Wasserstein 거리와 Fisher-Rao 거리를 활용, kinetic energy와 energy of growth를 설명
    • 목적 함수의 최소화 위해 유전자 발현 공간의 고차원 적분 계산 필요
      • high dimensionality 문제를 해결하기 위해, WFR 기반 동적 불균형 OT 문제에 dimensionless 형태의 수식화 도입
      • 두 개의 신경망을 사용해
        velocity \(v(x, t) = NN_1(x, t)\)
        growth \(g(x, t) = NN_2(x, t)\)
        로 근사
      • 수식화는 ODE의 시스템으로 귀결 ⟶ neural ODE(신경망 기반 ODE)로 최적화 및 해결
  • 세포 궤적을 추적하기 위해 TIGON은 velocity field를 따라 적분하여, progenitor(전구세포) 상태에서 descendant(후손세포) 상태까지의 동역학 추적
  • 유전자 분석은 상태 변수 \(x\)(유전자)가 속도와 성장에 어떻게 영향을 주고 기여하는지 설명
    • sigle-cell resolution(단일 세포 수준) 또는 cell-type level(세포 유형별)로 수행
    • 여러 세포 집단에 대해 평균값 계산, 무작위성 줄이고 추론의 강건성(robustness) 높임
  • GRN
    • directed(방향성), signed(부호), weighted(가중치)가 있는 그래프로 구성
      • edge의 방향: 유전자 간 조절 관계
      • edge의 부호: activation / inhibition
    • self-regulation 포함
    • 속도의 Jacobian 행렬을 통해 조절 행렬(regulatory matirx)로부터 계산
      • \[J={\left\{\frac{\partial \mathbf{v}_{i}}{\partial {x}_{j}}\right\}}_{i,\,j=1}^{d}\]
        • \(\frac{\partial \mathbf{v}_{i}}{\partial {x}_{j}}\): \(j\)번째 유전자(source gene)가 \(i\)번째 유전자(target gene)에 미치는 조절 강도(regulatroy strength)
  • gradient of growth를 통해 각 유전자가 성장에 어떻게 기여하는지 평가
    • \[\nabla g={\left\{\frac{\partial g}{\partial {x}_{j}}\right\}}_{j=1}^{d}\]
    • gradient of growth: 유전자 발현 공간 내에서의 growth potential
    • 가장 값이 큰 항들은 growth-related genes로 정의
  • 차원 축소 기법 수행: UMAP, PCA, AE
    • PCA와 AE는 가역적(reversible)이고 미분 가능(differentiable)
      ⟶ gradient of growth를 직접 근사하고, regulatory matirx를 계산
  • 각 측정된 시점에서의 세포 집단(cell population) 입력 필요. 정보가 없는 경우에는 각 시간 지점에서 수집된 세포의 수가 해당 시점의 세포 집단을 대표한다고 가정

Benchmark on a three-gene model

  • TIGON의 기능 테스트, 기존의 trajectory inference 및 GRN 추론 방법들과 비교 실험 수행
    • 세 개의 유전자로 구성된 GRN을 기반으로 한 in-silico 확률 모델 사용
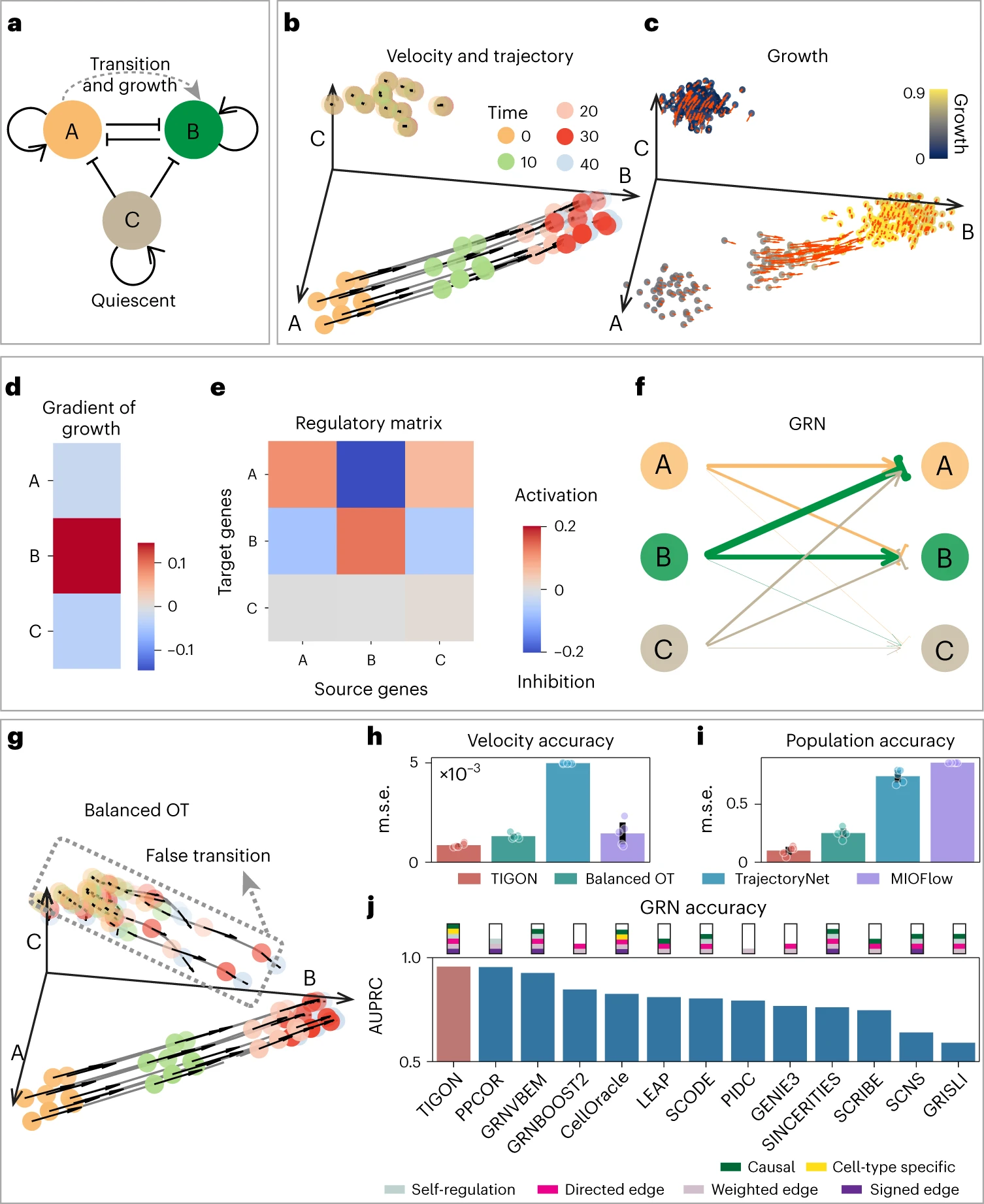
    • 모델은 세 가지 세포 상태(Fig.2a 참고)
    • 시뮬레이션은 서로 다른 역학(dynamics)을 가진 두 집단의 세포 생성(Supplementary Fig.1a 참고)
      • Supplementary Fig.1: Trajectory inference benchmark on simulated data 2
      • 첫 번째 세포 집단은 유전자 C가 높게 발현, 정지(quiescent) 상태
      • 다른 세포 집단은 상태 A에서 상태 B로 전이, B가 세포 분열을 촉진하여 세포 수의 증가(population growth) 유도

3

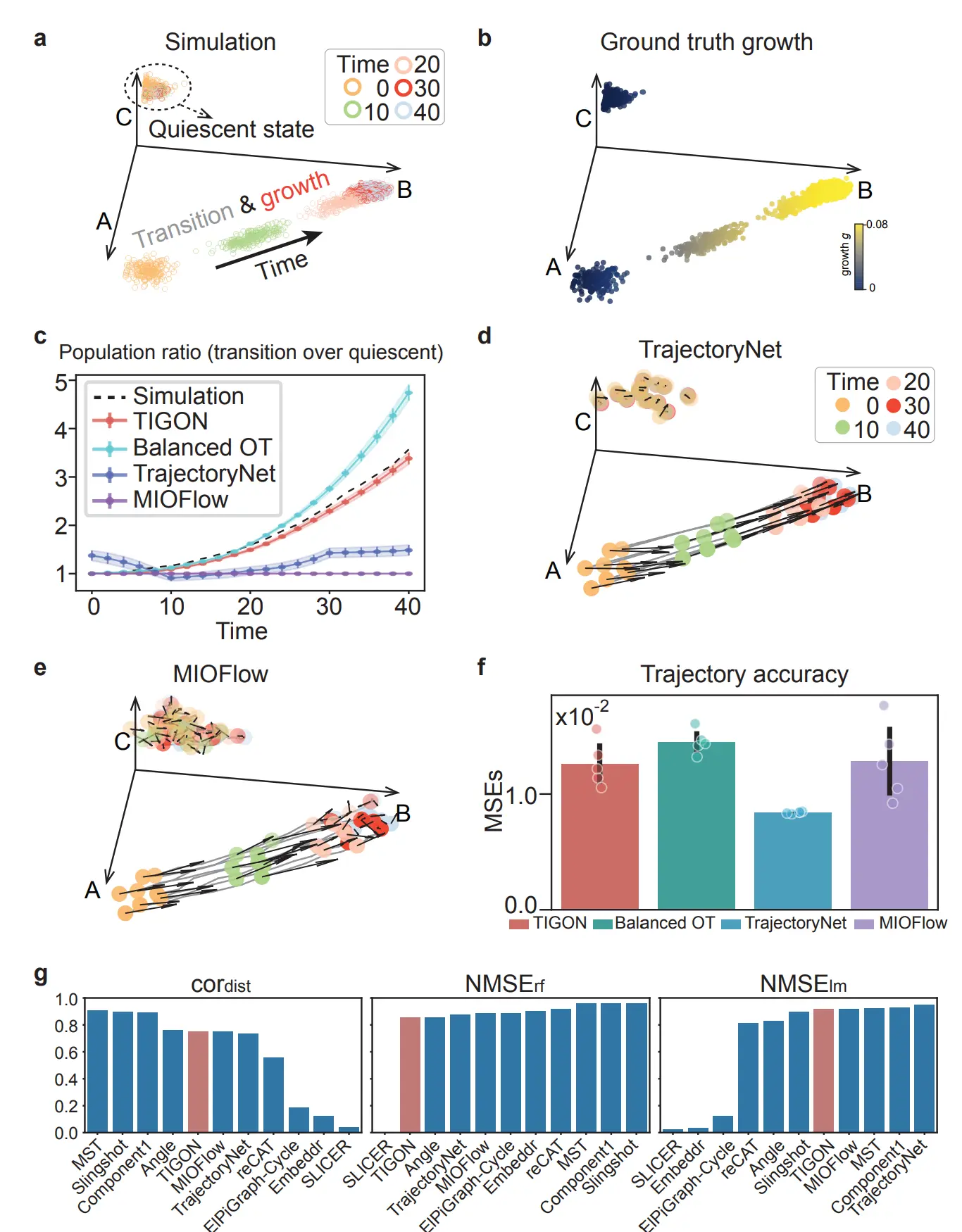
  • Fig.2: TIGON’s performance on three-gene simulated data
    • (a): 세 유전자 모델의 GRN을 도식화
    • (b): 시점 t=0에서 샘플링된 세포들의 세포 역학(dynamics)
      • 세포의 속도(검은 화살표)와 궤적(회색 곡선). 시점 t=0 초기 밀도에서 무작위로 20개의 세포 샘플링.
    • (c): 시점 t=0에서 샘플링된 세포들의 세포 역학(dynamics)
      • 성장 값(색으로 구분)과 성장의 기울기(붉은 화살표). 시점마다 100개의 세포 샘플링.
    • 전이 중인 세포들(transition cells)에 대한 유전자 분석
      • (d): 성장의 기울기
      • (e): 조절 행렬(regulatory matrix)
      • (f): GRN을 weighted directed graph 형식으로 시각화
        • 화살표 종류는 activation/inhibition 을, 선의 굵기는 regulatroy strength를 나타냄
    • (g): TIGON에서 성장 항(growth term)을 이동시키는 방식으로 균형 최적 수송(balanced OT)을 통해 추론된 속도 및 궤적
      • (b)와 동일한 20개의 세포(t=0 기준) 사용
    • TIGON과 다른 OT 기반 궤적 추론 방법들의 성능 비교
      • 정확도는 m.s.e.로 측정
      • 오차 막대는 각 방법에 대해 n=5번의 독립 실험에서 평균 대비 표준편차(1±SD)
      • 각 점은 반복 실험별 정확도
      • (h): 속도 예측 정확도에 대한 비교
      • (i): 전이 세포와 정지 세포간 세포 비율 예측 정확도에 대한 비교
    • (j): GRN 추론 기법들 간의 비교
      • 전이 세포에 대해 시점 t=0, 10, 20, …, 40에서 계산된 GRN을 기반으로 평가
      • 막대그래프는 시점 전반에 걸친 GRN 엣지 분류 정확도의 평균, 정밀도-재현율 곡선 하의 면적(AUPRC)으로 정량화
      • 각 방법의 기능은 막대 위의 사각형 박스에 요약
  • 시뮬레이션된 데이터 다섯 개 시점(snapshots)을 활용하여 TIGON은 두 개의 세포 집단(Fig.2b)과 성장 정보(Fig.2c)를 추론 ⟶ 정답 데이터(ground truth)와 일치
    • 분석 결과 성장을 촉진하는 유전자는 gene B(Fig.2d). TIGON은 A 상태에서 B 상태로 전이 중인 세포에 대한 세포 유형 특이적 GRN을 재구성(Fig2.e,f 및 Supplementary Fig.2a,b 참고)
    • Supplementary Fig.2: TIGON’s performance on simulated data 4
      • (a): regulatory matrix
      • (b): GRN in form of weighted directed graph
    • 전이 중인 세포들에서는 gene A와 gene B가 서로 강하게 억제(inhibit)하는 것으로 나타났고, gene C는 규제 기능이 거의 없으며 발현 수준도 0에 가깝게 유지됨 ⟶ gene A와 B 가이의 전환 스위치(toggle-switch)형 상호작용을 정확히 포착
  • TIGON과 세가지 최적 수송(OT) 기반 궤적 추론 방법 비교(Fig.2g-i)
    • 전이 중인 세포가 분열함에 따라, 전이 세포와 휴지기(quiescent) 세포의 비율이 증가(Supplementary Fig.1c)
    • TIGON은 성장과 속도를 함께 고려하기에 세포 궤적의 동역학과 세포 집단 비율을 정확히 포착
    • TIGON에서 성장 항(g)를 제거해 만든 Balanced OT 모델은 정지 상태의 휴지기 세포를 예측하지 못해 세포 집단 변화에 대한 보상으로 잘못된 전이(false transition)가 나타남(Fig.2g 및 Supplementary Fig.1c)
    • TrajectoryNet25와 MIOFlow26 같은 다른 balanced OT 기반 모델들은 서로 다른 목적 함수와 추가 정규화 항을 사용하여 잘못된 전이를 피함(Supplementary Fig.1d,e). 하지만 모델들이 계산한 속도는 휴지기 상태나 전이 후반 단계에서 방향성이 무질서하며, 크기도 비정상적으로 큼. 또한 세포 집단 비율이 실제와 달리 거의 변화하지 않아 정답(ground truth)과 일치하지 않음(Supplementary Fig.1c)
    • 전반적으로 TIGON은 속도와 세포 집단 비율 예측에서 더 높은 정확도를 보이며(Fig.2h,i), TrajectoryNet은 궤적 예측에서 더 뛰어난 성능(Supplementary Fig.1f)
  • 단일세포 의사시간(pseudogime) 분석 기번들과도 표준 벤치마크 지표를 활용, 비교 진행(Supplementary Fig.1g)
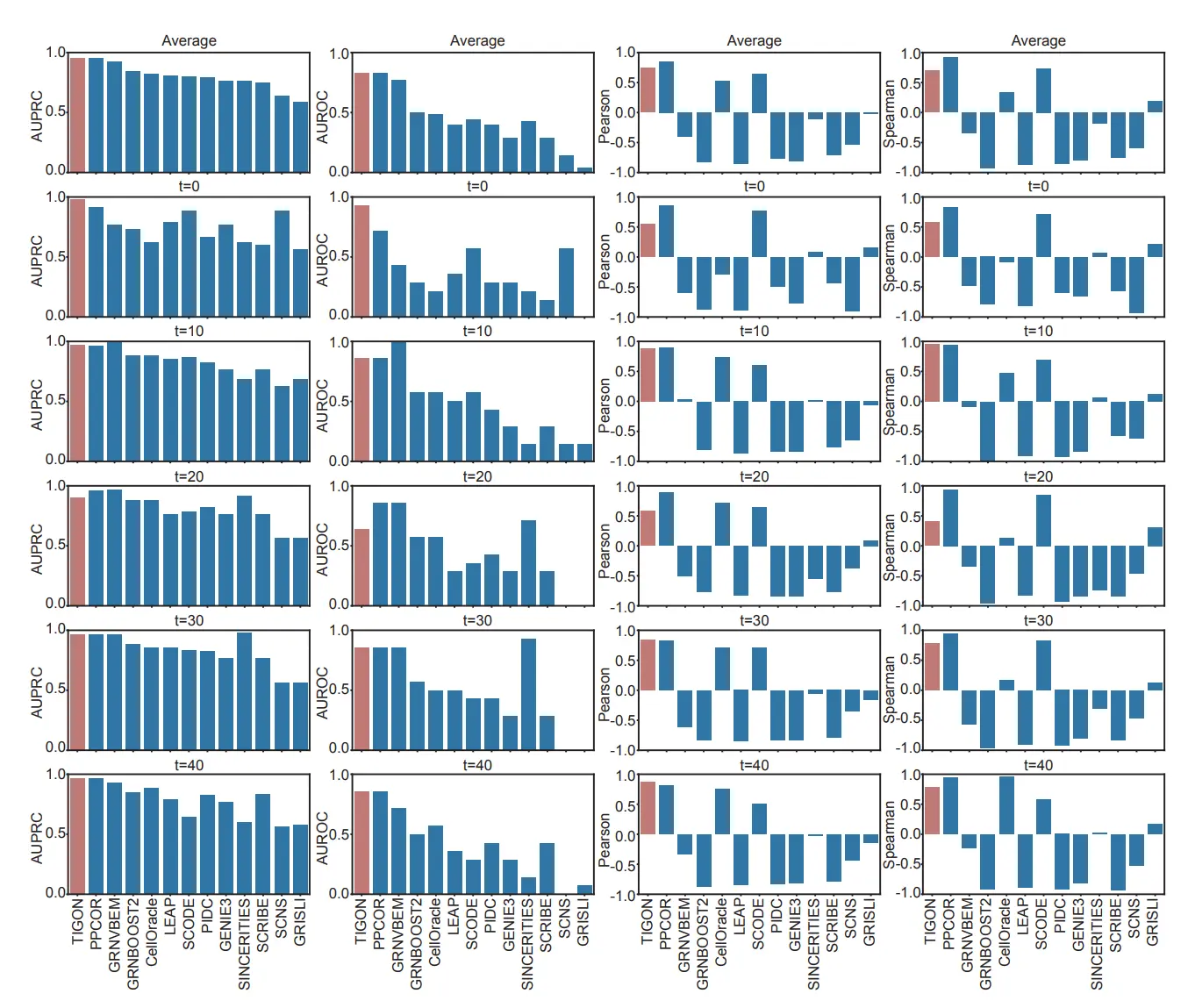
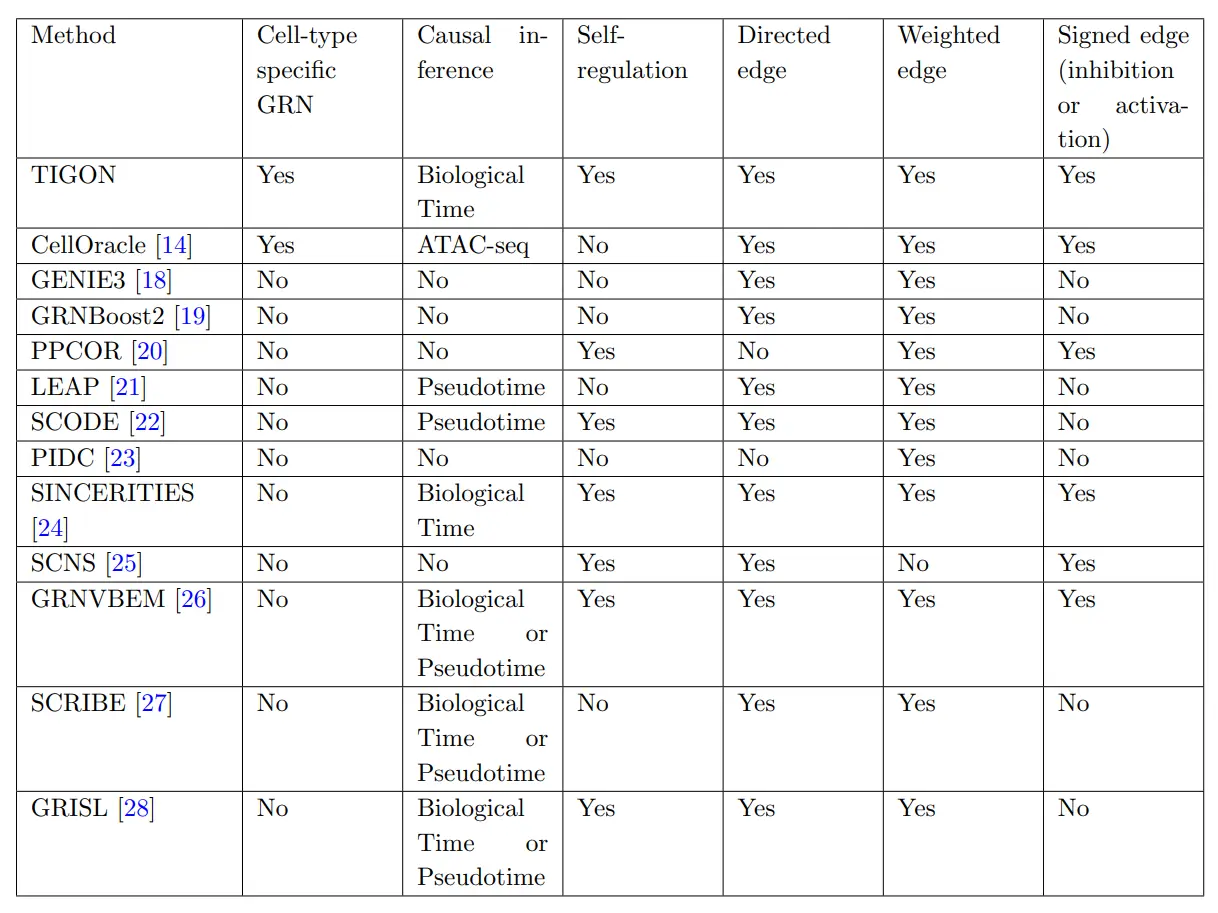
  • TIGON과 다른 12가지 GRN의 추론 네트워크 비교
    • 인과 관계(causal effects)와 세포 유형 특이적 GRN을 모두 고려하는 것은 TIGON과 CellOracle. 특히 TIGON은 특정 유전자의 자기 조절(self-regulation)까지 포함한 보다 완전한 네트워크 구조(Fig.2j, Supplementary Fig.3 및 Supplementary Table 1)
    • Supplementary Fig.3: Gene regulatory network inference benchmark on simulated data 5
    • Supplementary Table 1: Summery of GRN inference methods 6
    • 종합적으로 BEELINE 벤치마크에서 GRN 내 방향성 있는 엣지를 분류하기 위해 사용하는 두가지 지표(AUPRC: 정밀도-재현율 곡선 아래 면적, AUROC: 수신자 조작 특성 곡선 아래 면적) 모두에서 TIGON이 가장 높은 값 기록
    • TIGON은 방향성과 부호를 가진 GRN 엣지의 가중치를 예측할 때, 피어슨 상관계수에서는 두 번째로, 스피어만 상관계수에서는 세 번째로 높은 성능

Model predictions align with lineage tracing experiments

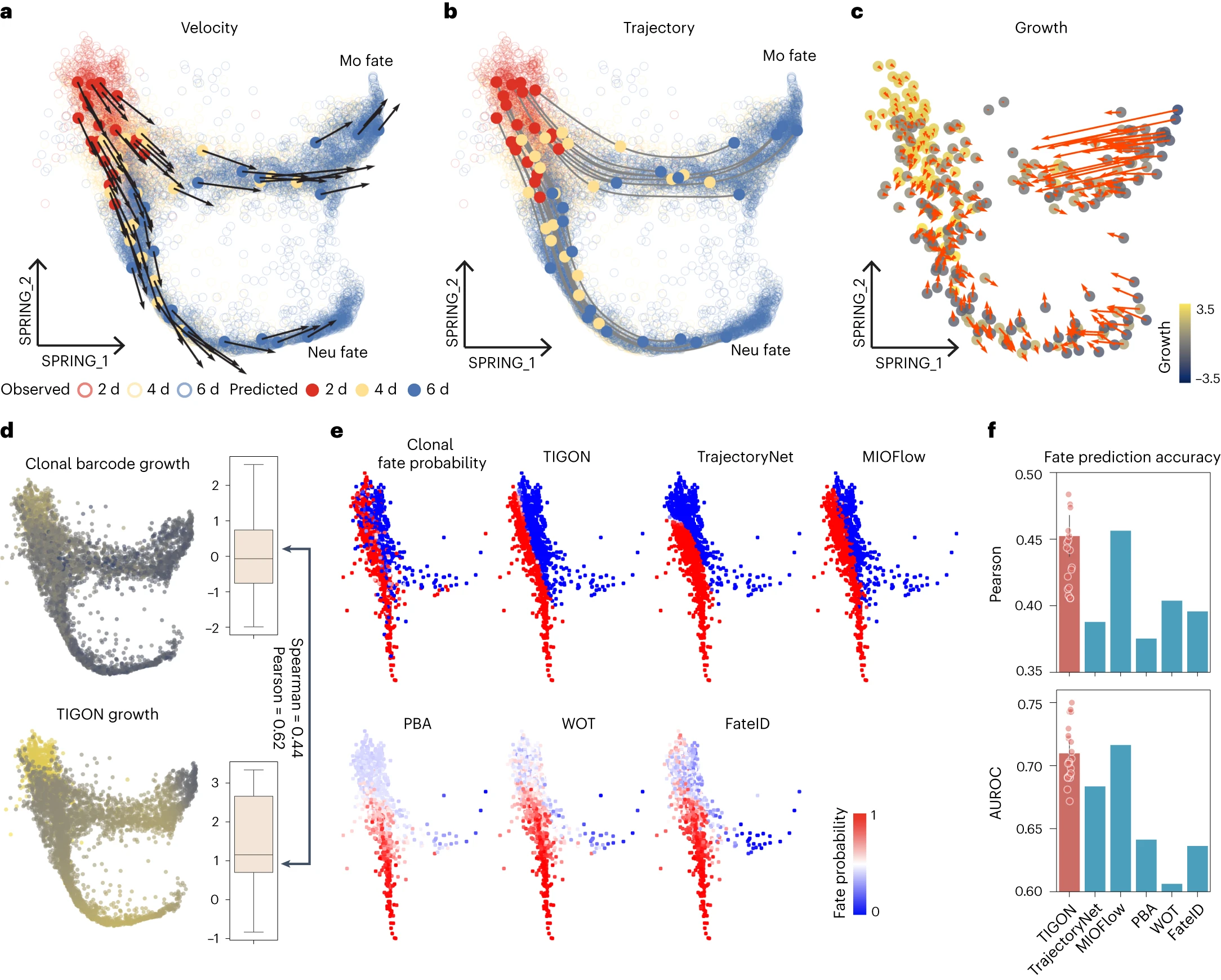
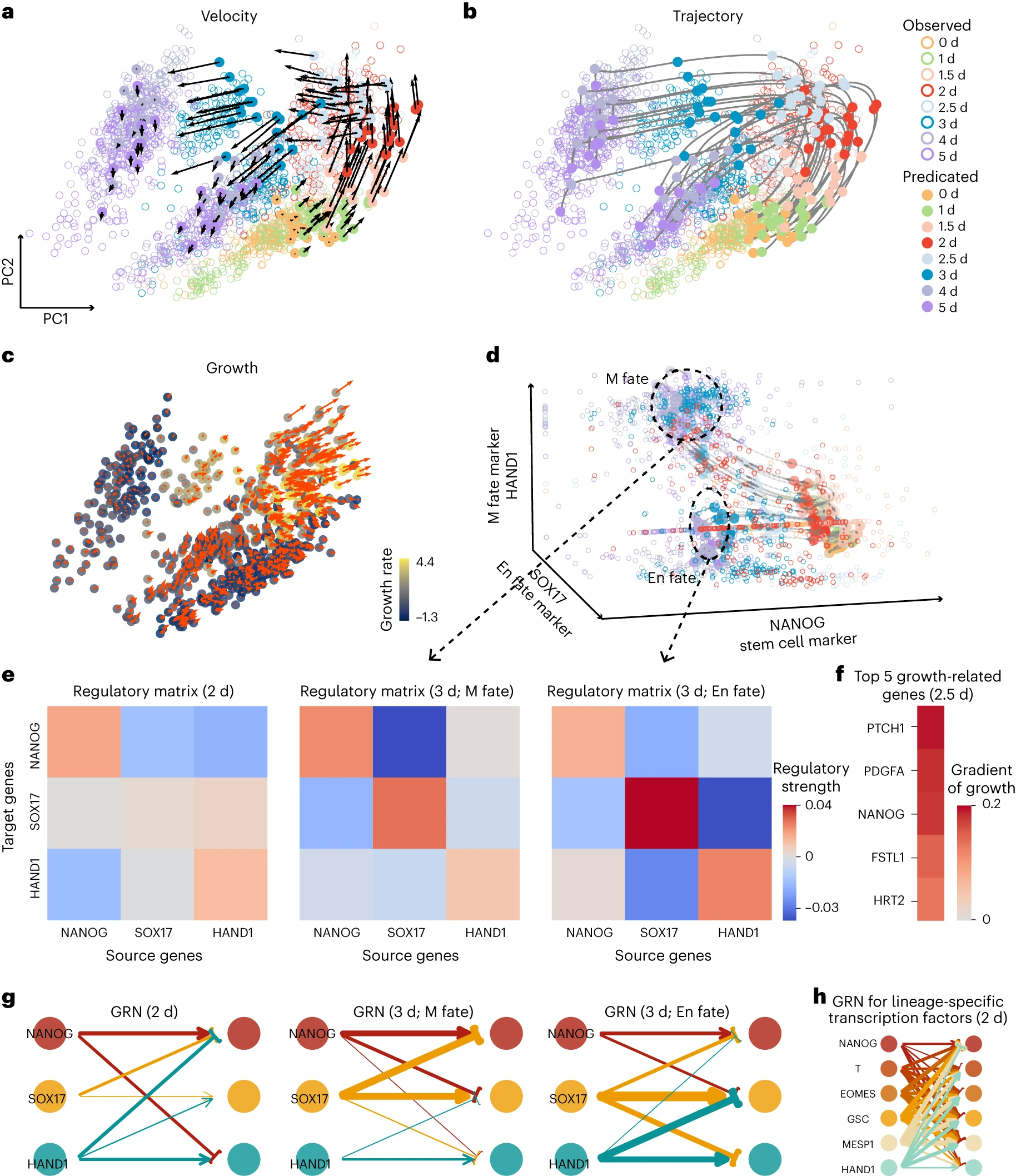
  • TIGON을 생쥐 조혈(hematopoiesis)과정의 시계열 scRNA-seq 데이터에 적용, lineage tracing 기법 사용
    • 데이터셋은 추가적인 barcode를 이용해 시간에 따라 클론 추적. 동일 클론에 속한 세포들은 0일차에 동일한 조상 세포(progenitor cell)에서 유래했기에 세포의 궤적과 성장에 대한 정보 제공
    • 기존 연구(Lineage tracing on transcriptional landscapes links state to fate during differentiation)를 따라 2일차, 4일차, 6일차 시점에서 호중구(neutrophils, Neu)와 단핵구(monocytes, MO)운명으로 분화하는 클론 내 세포 선택
    • 초기 단계부터 분화의 방향성과 속도 감지, 실제 클론 기반 성장값과 비교했을 때 높은 상관도(spearman 상관계수 0.44, pearson 상관계수 0.62)

  • Fig 3: TIGON’s performance on the lineage tracing dataset

    7

    • force-directed layouts (SPRING plots)
      • solid dots: TIGON에 의해 예측된 세포들, 2일차의 세포 밀도에서 초기로 20개 샘플링
      • circle: 실제 scRNA-seq 데이터에서 관측된 모든 세포
      • 세 시점의 스냅샷이 서로 다른 색으로 표시
        • (a): 세포의 속도
        • (b): 세포의 궤적
      • (c): 세포의 성장 및 성장 기울기
        • 각 시점(2일, 4일, 6일)의 밀도 분포에서 무작위로 샘플링한 100개의 세포 시각화
    • (d): Spring plot을 사용해 cloanal barcode와 TIGON에 의해 추정된 2일차와 3일차의 세포 성장 값 비교
      • 박스플롯은 총 5,120개의 세포 성장값 분포 요약
    • (e): 2일차 세포에 대해 Neu fate을 추정한 결과의 확률값
      • clonal fate probability(클론 바코드 기반 운명 확률)는 ground truth으로 사용
    • (f): 클론 기반 운명 확률을 예측한 정확도를 barplot으로 표현. 산점도는 각 반복 실험에서의 정확도
      • 위쪽: Pearson correlation 기준
      • 아래쪽: AUROC 기준
  • TIGON과 다른 trajectory inference 방법들과 비교
    • lineage 데이터는 클론 단위로 세포의 궤적을 추적하는 반면, 계산 기반 방법들은 개별 세포 단위로 궤적을 추론. 계산된 궤적에 대해 ground truth은 없지만 각 세포에 대한 fate probability을 실험값과 계산값 간에 비교 ⟶ 2일차에 해당 클론 후손 세포 중 얼마나 많은 세포가 호중구(Neu) 운명으로 분화했는지를 바탕으로, 실험 기반 클론 운명 확률 계산
  • TIGON은 실험적 클론 운명 확률과 유사한 이진적 패턴 재현, 상관계수 및 AUROC에서도 정확도가 뛰어남(Fig3.e,f)
  • TrajectoryNet, MIOFlow는 상위권 성능을 보이지만 PBA, WOT, FateID는 불확실한 결과

Reconstructing cellular dynamics in EMT

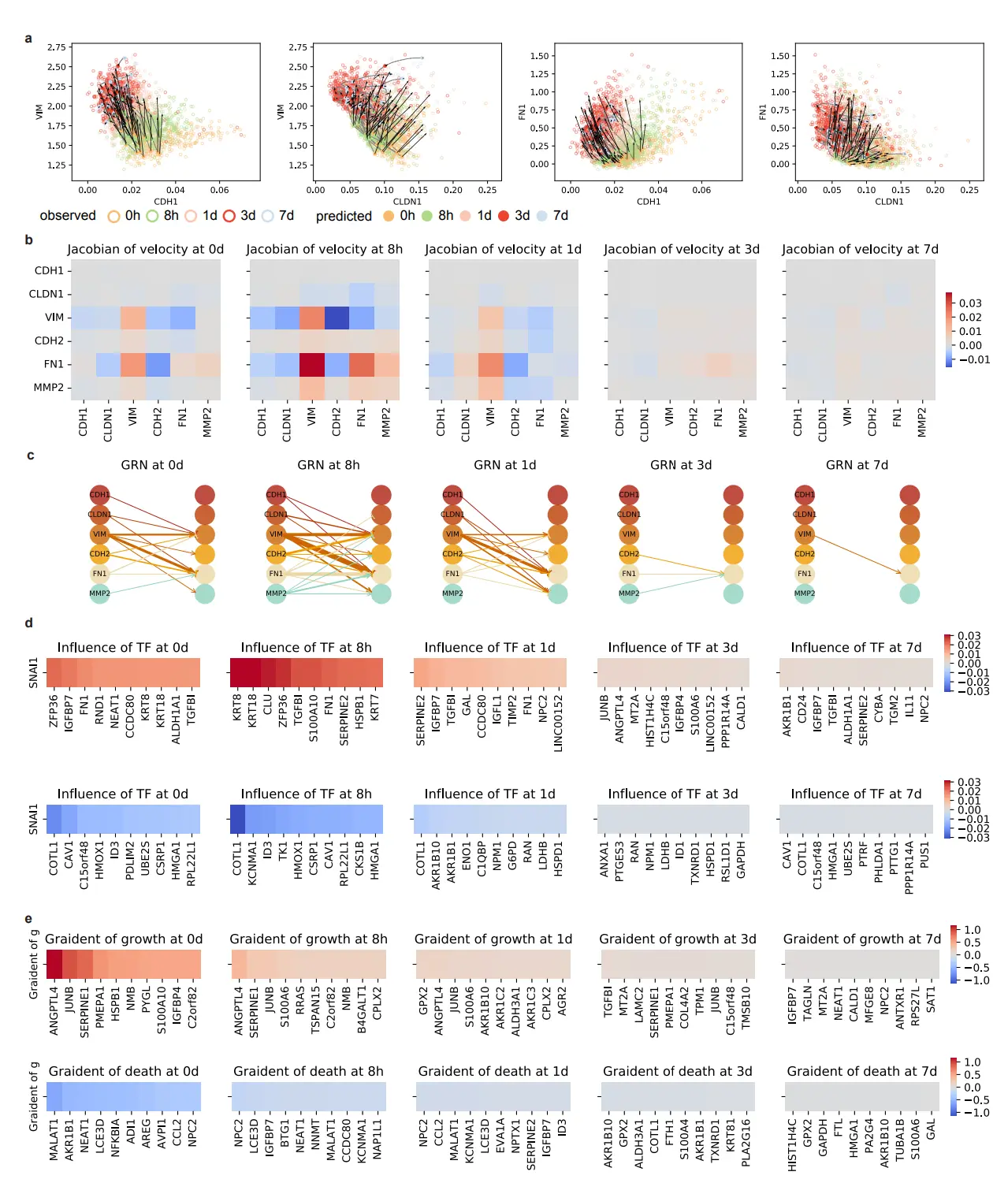
  • TIGON을 A549 암세포주에서 수집된 시계열 scRNA-seq 데이터에 적용
    • 10차원의 잠재 공간(latenet space)을 갖는 오토인코더(AE)를 학습시켰고, 이 잠재 공간을 TIGON의 입력으로 사용
    • 출력 결과의 시각화를 위해 10차원 잠재 공간을 2차원 UMAP으로 다시 투영
  • 시계열 데이터는 초기의 상피세포(epithelial cells, E)가 중간 상태(intermediate state)를 거쳐 최종적으로 간엽세포(mesenchymal state, M)로 분화 ⟶ TIGON이 추론한 궤적은 이와 유사한 전이 동역학 재현

  • 중간 상태에서의 성장 증가는 줄기세포성과 관련된 기존 생물학적 발견과도 부합

  • Fig 4: TIGON’s performance ont the EMT scRNA-seq dataset 8

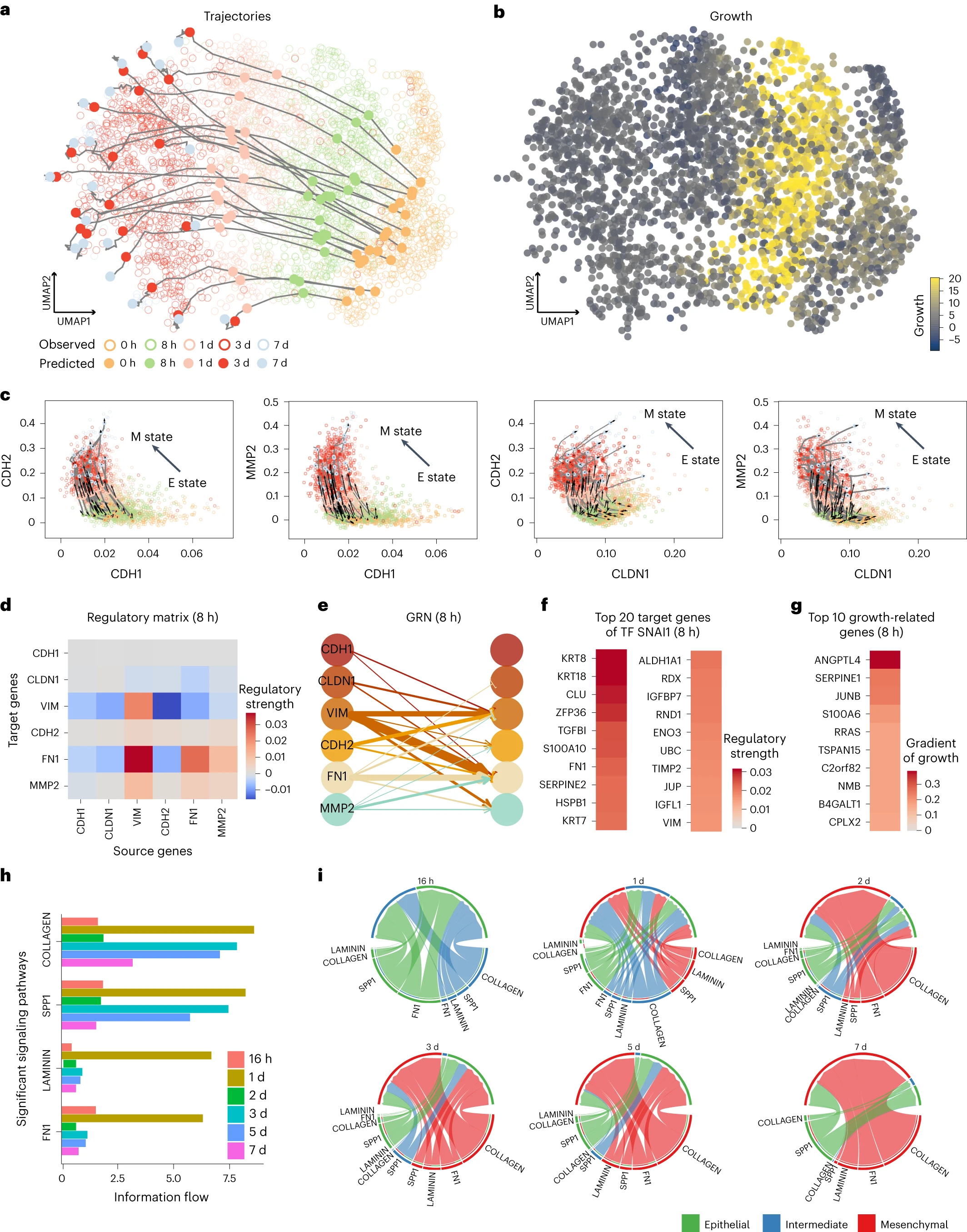
    • 분석 결과는 AE로부터 얻어진 10차원 latent space을 기반으로 도출
    • TIGON의 출력 결과를 UMAP 공간에 시각화
      • (a): 0시간 시점의 밀도 분포에서 무작위로 샘플링한 20개의 세포의 궤적
      • (b): 관측된 모든 세포에 대한 성장값(growth value)을 색으로 시각화한 결과
    • (c): 유전자 발현 공간에서 세포의 궤적과 속도. (a)에서의 세포를 표시
    • 8시간 시점에서 EMT 마커 유전자 6개에 대한 결과
      • (d): regulatory matrix
      • (e): GRN
    • (f): 8시간 시점에서 EMT 관련 전사인자(TF)인 SNAI1의 상위 20개 타겟 유전자에 대한 regulatory matrix
    • (g): 8시간 시점에서 성장과 관련된 상위 10개 유전자에 대한 gradient of growth
    • (h): CellChat 분석을 통해 추론된 네 가지 주요 신호 전달 경로의 정보 흐름을 막대그래프로 표현
    • (i): CellChat 분석을 통해 서로 다른 시간대에서 상피, 중간, 간엽 세포 간에 발생한 cell-cell communication을 chord diagram으로 표현
  • 두 개의 E 마커 유전자와 네 개의 M 마커 유전자가 포함된 GRN 추가로 분석
    • E 마커 유전자로부터 M 마커 유전자에 대한 억제 작용 관찰(Fig.4d,e 및 Supplementary Fig.4b,c)
      • Supplementary Fig.4: TIGON’s performance on EMT dataset using ten-dimensional autoencoder latent space 11
  • 전사인자(TF)가 타겟 유전자에 미치는 시간적 인과 효과를 분석한 결과, EMT에서 대표적인 전사인자인 SNAI1이 VIM과 FN1에 대해 양의 조절 효과를 보이는 것을 확인. SNAI1의 추가적인 잠재적 타겟 유전자들도 예측(Fig.4f 및 Supplementary Fig.4d)
  • 성장 관련 상위 10개 유전자 중 5개가 실제로 세포 성장에 관여(Fig.4g)

  • TIGON이 추론한 세포 동역학은 실제로 측정되지 않은 시점의 단일세포 유전자 발현 수준까지 제공

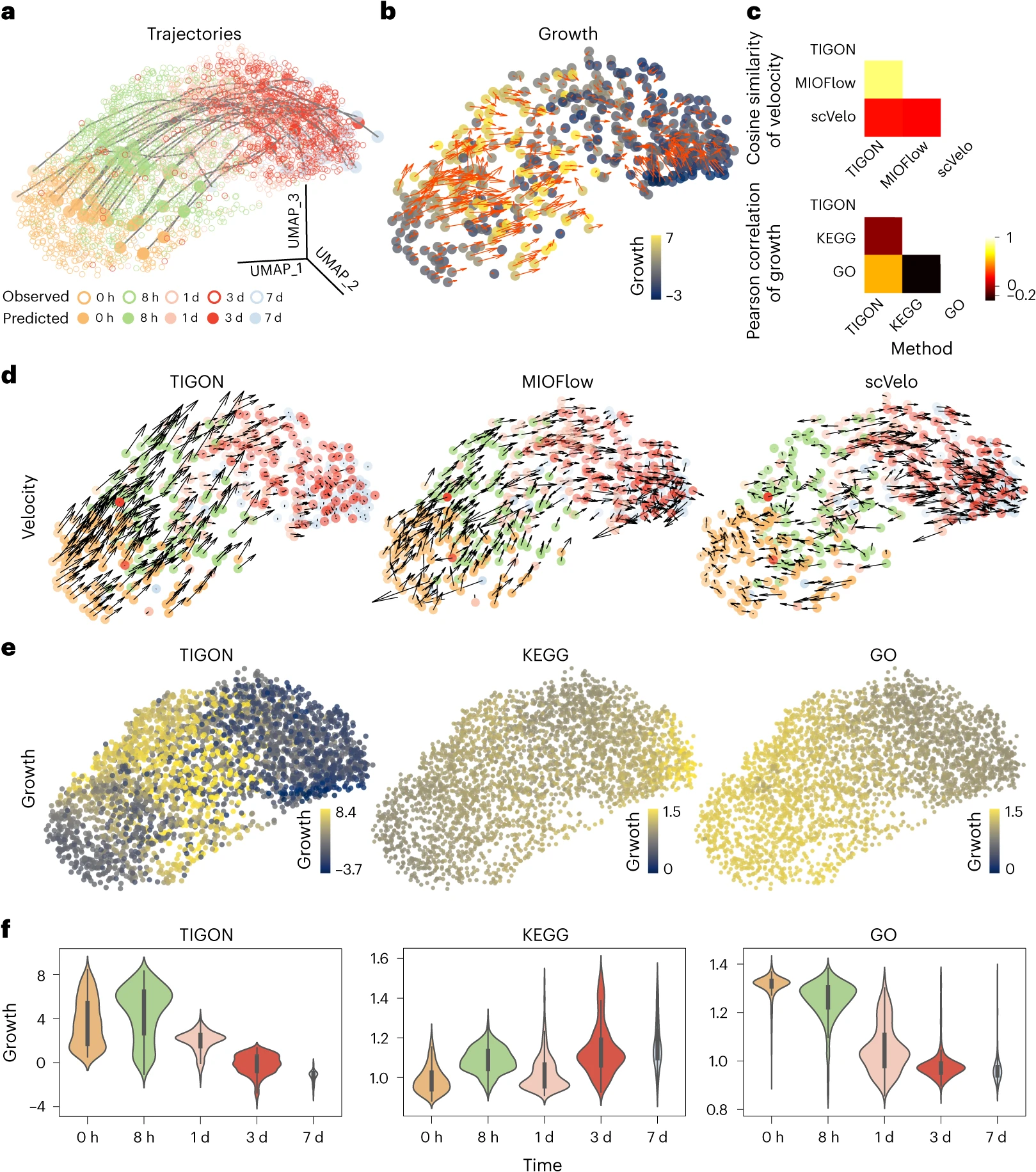
  • Fig 5: Comparisons of TIGON with trajectory inference or growth inference methods on the EMT scRNA-seq dataset 9

Identifying bifurcation of directed differentiation in iPSCs

  • Fig 6: TIGON’s performance on the single-cell qPCR iPSC dataset with bifurcation 10

Discussion

  1. 개요 및 목적
    • TIGON: scRNA-seq에서 세포 성장 및 유전자 발현 속도를 동시 추론하는 딥러닝 기반 동적 모델
    • WFR 거리를 이용한 동적 비평형 최적수송(OT) 방식을 적용하여, 세포 분열과 사멸 모델링
  2. 적용 가능한 분야
    • scRNA-seq 외
    • 단일 세포 ATAC-seq
    • 공간 전사체 데이터
    • Image-to-image translation 등 고차원 OT 문제에 활용 가능
  3. 차원 축소 기법
    • 가역적(재구성 가능)차원 축소 기법 사용 필요
    • AE, PCA, Reversible UMAP
    • 재구성 정확도를 바탕으로 적절한 잠재 공간 차원(latent dimension) 설정
    • Elbow plot 또는 AE 재구성 오류 그래프로 적정 차원 도출
  4. TIGON의 최적화 목적함수
    • 재구성 오류와 WFR 걸이 기반 비용 함수 결합
    • 단기 및 재구성 오류 모두 고려 ⟶ 다양한 시간 스케일의 통합 오류 감소
    • WFR 내 Wasserstein 대 Fisher-Rao 가중치 조정으로 결과의 일관성과 강건성 확보
  5. 고차원 OT 해결 방법
    • 기존 mesh-based 방법은 고차원에서 계산량 폭증(O(N^d))
    • TIGON은 mesh-free 딥러닝 접근법을 통해 10차원 이상 OT 문제 해결 가능
    • 향후 더 높은 차원(\(10^3\) ~ \(10^4\)) 문제에는 메모리 효율적 뉴럴 ODE와 안정적 수치 해법 필요
  6. 전처리와 데이터 품질 요구사항
    • 배치 효과(batch effect) 제거 필수: 원 논문 제공 embedding 사용 or Seurat 프로토콜 사용
    • 차원 축소 전처리 결과의 품질 중요
    • 충분한 세포 수와 시간 포인트, 낮은 초기 세포 밀도 분산 필요
  7. 성장 추론 및 세포 간 전이
    • TIGON은 성장 유전자 리스트 없이도 성장률 추정 가능
    • 성장 gradient와 전이 velocity 사이의 양의 코사인 유사도 ⟶ 성장과 전이의 시너지 반영
  8. 모델 개선 방향
    • cell potency 기반 정규화 적용
    • RNA velocity, unspliced RNA 데이터로 전이 제약 조건 강화 가능
    • cell-cell communication 직접 모델링은 도전 과제
    • TIGON 예측 결과에 CellChat, exFINDER 등 도구 적용 가능 ⟶ 시간 기반 신호 네트워크 재구성
  9. 총평
    • TIGON은 시간적 단일세포 유전자 발현 데이터를 이용하여 세포 역학 및 GRN을 추론할 수 있는 강력한 도구. 차원 축소, 성장 추론, 동적 OT 해법, 딥러닝 기반의 고차원 문제 해결 능력은 다양한 오믹스 분야에 응용 가능성 존재.

Code availability

Biology, System dynamics
paper
This post is licensed under CC BY 4.0 by the author.